Research Areas & Expertise
Computational Mathematics: The Foundation of Modern AI
My expertise in computational mathematics forms the mathematical foundation that powers modern artificial intelligence and machine learning systems. The algorithms, numerical methods, and mathematical frameworks I work with are fundamental to AI development, from neural network optimization to large language models (LLMs) and scientific computing applications.
- Computational and Applied Mathematics
- Computer Science, Distributed Computing, AI and Machine Learning
- Numerical Analysis and Scientific Computing
- Numerical Solutions to Partial Differential Equations
- Numerical Linear Algebra and Matrices
- Shock Waves, Supersonic Flows, and Aerodynamics
- Computational Fluid Dynamics (CFD)
- Multiscale and Multiphase Systems
- Continuum Mechanics and Elasticity
- Electromagnetics and Semiconductor Physics
- Mathematical Physics and Differential Equations
- Mathematical Biology
- Financial Mathematics and Quantitative Analytics
- Data Analytics and Statistical Modeling
- AI and Machine Learning (Neural Networks, LLMs)
- Large Scale Distributed Computing
- Software Engineering and Reliable System Design
- Semiconductor Research and Nanotechnology
Graduate Research: Numerical Modeling of Shock-Induced Cavity Collapse
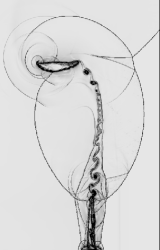
My doctoral research focused on advanced computational modeling of shock wave interactions with gaseous cavities in solid matrices, a phenomenon known as bubble collapse in supersonic regimes.
- Bubble Collapse Dynamics: Developed sophisticated mathematical models and computational algorithms for simulating the interaction between strong shock waves and gaseous cavities within solid matrices. Extended computational fluid dynamics (CFD) software frameworks to handle multi-material configurations with robust interface tracking capabilities.
- Discovery of Tall-Bubble Collapse Mechanism: Identified and characterized a novel collapse mechanism resulting from geometric interface variations. This discovery revealed the generation of extremely high pressure and temperature concentrations, sufficient to trigger deflagration-to-detonation transitions and other high-energy phenomena such as Inertial Confinement Fusion (ICF).
Simulation Videos
Publications
- Ozlem, M., Kapila, A.K., Schwendeman, D.W., Henshaw, W.D. (2011). "A Numerical Study of Shock-Induced Cavity Collapse." Shock Waves, Springer.
- Ozlem, M., Kapila, A.K., Schwendeman, D.W., Henshaw, W.D. (2010). "A Numerical Study of Shock-Induced Cavity Collapse." Doctoral Dissertation, Rensselaer Polytechnic Institute.
- Ozlem, M. (2010). "Numerical Modeling of Shock-Induced Cavity Collapse." Ph.D. Thesis, Rensselaer Polytechnic Institute.
- Ozlem, M. (2007). "Maximizing Minimum Pressure in Fluid Dynamic Bearings of Hard Disk Drives." 23rd Annual Workshop on Mathematical Problems in Industry, University of Delaware.
- Ozlem, M. (2007). "My Air Conditioner? You're Standing on it!" Graduate Student Mathematical Modeling Camp, Rensselaer Polytechnic Institute.
- Patent: "Method and system for template pattern optimization for dsa patterning using graphoepitaxy" (14/723570, Disclosure # YOR820130312, Docket # YOR920150102US1)
Invited Presentations
- "Shock Induced Single Bubble Collapse." Applied Math Days, Rensselaer Polytechnic Institute, March 2010.
- "Numerical Multi-Material Flow and Shock Wave-Bubble Void Interactions: Effects of Hydrodynamic Void Collapse on Ignition Process." Applied Math Days, Rensselaer Polytechnic Institute, November 2008.
- "Numerical Modeling of Void Collapse: Shock Wave and Gas Bubble Interaction." SIAM Gators Conference, University of Florida, March 2009.
Education
- Ph.D. in Mathematics (GPA: 3.95/4.0)
- M.S. in Applied Mathematics (GPA: 4.0/4.0)
- B.A. in Mathematics and Computer Science (GPA: 3.98/4.0)
Professional Experience
- Adjunct Professor
- Teaching Assistant
- Research Assistant
- Mathematical Modeling
- Software Engineering and Reliable System Design
Academic Background